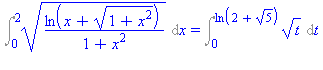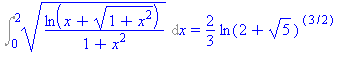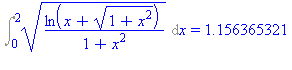Az integrálszámítás alaptétele
Ha az f függvénynek van elemi függvényként megadható primitív függvénye, akkor a határozott integrál ennek segítségével könnyen kiszámítható. A kiszámítás alapja a Newton-Leibniz tétel. A tételt a Lagrange-tétel felhasználásával bizonyítjuk. Ezért elõzõleg átismételjük az utóbbi tételt.
Lagrange-tétele
Tétel. (Lagrange tétele)
Ha 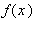 az
az ![[a, b]](images/Newton_Leibniz_2.gif) zárt intervallumon folytonos és
zárt intervallumon folytonos és
az ( a,b ) nyílt intervallumon differenciálható,
akkor az ( a,b ) intervallumban van olyan 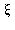 amelyre
amelyre
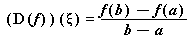 .
.
Másképp jelölve
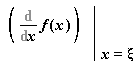 =
= 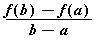
A tétel szerint a feltételeket teljesítõ f függvény esetén van az (a,b) intervallumban olyan 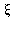 hely, ahol a függvény változási sebessége egyenlõ az
hely, ahol a függvény változási sebessége egyenlõ az ![[a, b]](images/Newton_Leibniz_8.gif) intervallumbeli átlagos változási sebességgel. Geometriailag ez azt jelenti, hogy az adott pontbeli érintõ párhuzamos az intervallum végpontjaihoz tartozó szelõvel.
intervallumbeli átlagos változási sebességgel. Geometriailag ez azt jelenti, hogy az adott pontbeli érintõ párhuzamos az intervallum végpontjaihoz tartozó szelõvel.
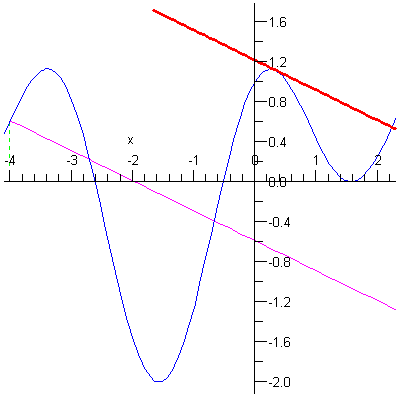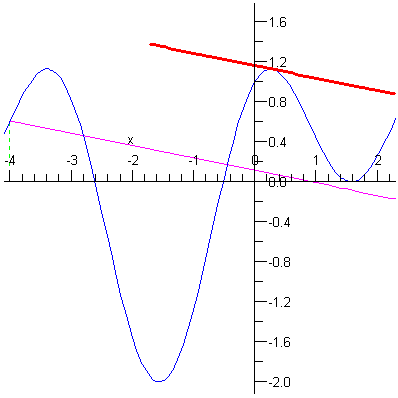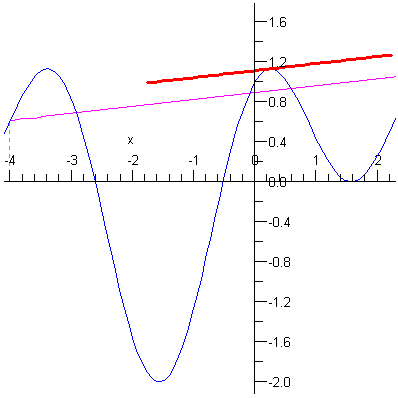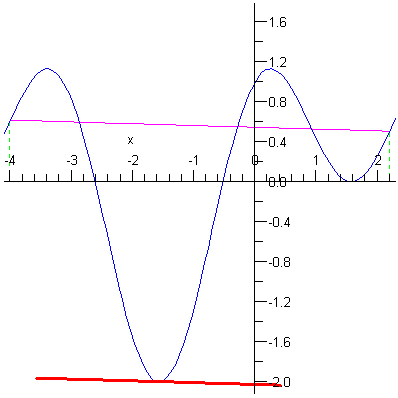
Az alábbi Langrange eljárás a Langrange tételt állítását szemlélteti. A feltételek teljesülése esetén ábrázolja a szelõt és a vele párhuzamos érintõt, egyébként pedig hibaüzenetet küld.
| > |
Lagrange:=proc(f,a,b)
local abra1,abra2, vonal1, vonal2, xi, szelo:
if not(iscont(f(x),x=a..b,'closed')) then
ERROR(`Nem folytonos az [a,b] zárt intervallumon`):
fi:
if not(iscont(D(f)(x),x=a..b)) then
ERROR(`Nem deriválható az (a,b) nyílt intervallumon`);
fi:
xi:=fsolve(D(f)(x)=(f(b)-f(a))/(b-a),x=a..b);
abra1:=plot(f(x),x=a-0.1..b+0.1,color=blue):
abra2:=plot(D(f)(xi)*(x-xi)+f(xi),x=xi-2..xi+2,color=red,thickness=2):
vonal1:=plottools[line]([a,0],[a,f(a)],color=green,linestyle=3):
vonal2:=plottools[line]([b,0],[b,f(b)],color=green,linestyle=3):
szelo:=plot((f(b)-f(a))/(b-a)*(x-a)+f(a),x=a..b,color=magenta):
plots[display]([vonal1,vonal2,szelo,abra1,abra2])
end:
|
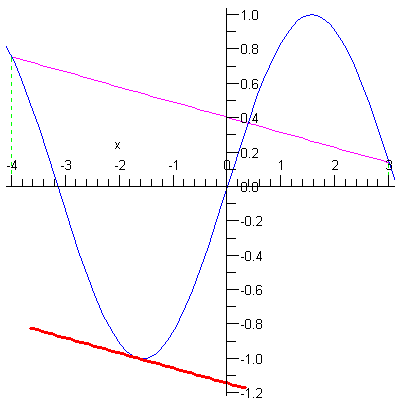
Hívjuk meg a Lagrenge eljárást a sin függvénnyel, a vizsgált intervallum legyen [-4,3] . Megjegyezzük, hogy a 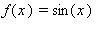 eljesíti a Lagrange tétel feltételeit, hiszen a színusz függvény a valós számos halmazán deriválható és így ott folytonos is.
eljesíti a Lagrange tétel feltételeit, hiszen a színusz függvény a valós számos halmazán deriválható és így ott folytonos is.
Javasoljuk kipróbálni más intervallumokon a Langrange eljárást. Ehhez csak az alábbi utasításban szereplõ intervallum végpontokat kell megvaltoztatnunk és újra végrehajtani az utasítást (értsd. leütni az Enter billentyût).
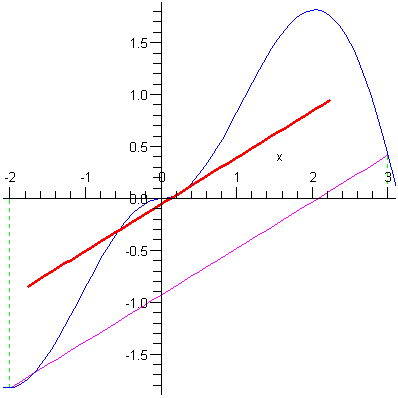
Az eljárás szakaszonként adott (
piecewise
) függvényekre is alkalmazható:
| > |
g:=x->piecewise(x<=0,-x*sin(x),x*sin(x)); |
![(Typesetting:-mprintslash)([g := proc (x) options operator, arrow; piecewise(x <= 0, -x*sin(x), x*sin(x)) end proc], [proc (x) options operator, arrow; piecewise(x <= 0, -x*sin(x), x*sin(x)) end proc]...](images/Newton_Leibniz_11.gif)
Tekintsünk egy példát arra az esetre, amikor a feltételek valamelyike nem teljesül:
Példa
Vizsgáljuk meg, hogy teljesülnek-e a Lagrange-tétel feltételei az
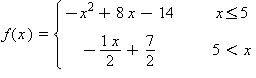
függvényre!
Megoldás
Vegyük föl a szakaszonként adott függvényt!
| > |
f:=x->piecewise(x<=5,-x^2+8*x-14,x>5,x^2-7*x+11); |
![(Typesetting:-mprintslash)([f := proc (x) options operator, arrow; piecewise(x <= 5, -x^2+8*x-14, 5 < x, x^2-7*x+11) end proc], [proc (x) options operator, arrow; piecewise(x <= 5, -x^2+8*x-14, 5 < x,...](images/Newton_Leibniz_14.gif)
![(Typesetting:-mprintslash)([f(x) = PIECEWISE([-x^2+8*x-14, x <= 5], [x^2-7*x+11, 5 < x])], [f(x) = piecewise(x <= 5, -x^2+8*x-14, 5 < x, x^2-7*x+11)])](images/Newton_Leibniz_15.gif)
Ábrázoljuk a függvényt és deriváltját közös koordinátarendszerben:
| > |
plot([f(x),D(f)(x)],x=4..6,discont=true,color=[blue,red],thickness=2,legend=["f(x)","D(f)(x)"]); |
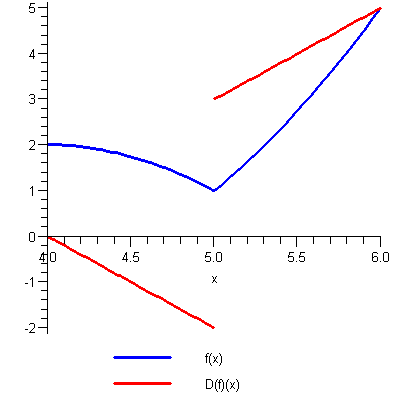
A függvény folytonos az ![[5, 7]](images/Newton_Leibniz_17.gif) intervallumon, az
intervallumon, az 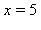 helyen azonban nem differenciálható.
helyen azonban nem differenciálható.

| > |
iscont(D(f)(x),x=4..6); |
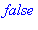
Error, (in Lagrange) Nem deriválható az (a,b) nyílt intervallumon
A következõ utasítássorozat különbözõ intervallumok egymásutánján animációval szemlélteti a Langrange tétel állítását.
![(Typesetting:-mprintslash)([f := proc (x) options operator, arrow; sin(x)+cos(2*x) end proc], [proc (x) options operator, arrow; sin(x)+cos(2*x) end proc])](images/Newton_Leibniz_21.gif)
| > |
p:=seq(Lagrange(f,-4,4.6-k*0.2),k=0..12): |
| > |
plots[display]([p],insequence=true); |
Newton-Leibniz tétel
Tétel
Ha 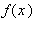 az
az ![[a, b]](images/Newton_Leibniz_24.gif) intervallumon integrálható (létezik határozott integrálja) és ezen az intervallumon primitív függvénye is van ( legyen ezek egyike
intervallumon integrálható (létezik határozott integrálja) és ezen az intervallumon primitív függvénye is van ( legyen ezek egyike 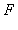 ), akkor
), akkor
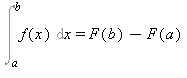
Bizonyítás
Tekintsük az ![[a, b]](images/Newton_Leibniz_27.gif) intervallum tetszõleges beosztását. Tekintve, hogy a F függvény a
intervallum tetszõleges beosztását. Tekintve, hogy a F függvény a 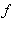 primitív függvénye az
primitív függvénye az ![[a, b]](images/Newton_Leibniz_29.gif) intervallumon, F deriválható az
intervallumon, F deriválható az ![[a, b]](images/Newton_Leibniz_30.gif) intervallumon, és annak bármely részintervallumán, s
intervallumon, és annak bármely részintervallumán, s 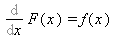 (
( 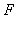 '(x)=
'(x)=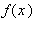 ). Ha a függvény deriválható, akkor folytonos. Ezért az F függvényre az
). Ha a függvény deriválható, akkor folytonos. Ezért az F függvényre az ![[a, b]](images/Newton_Leibniz_34.gif) bármely
bármely ![[x[i-1], x[i]]](images/Newton_Leibniz_35.gif) részintervallumán érvényes Lagrange tétele, tehát az
részintervallumán érvényes Lagrange tétele, tehát az ![[x[i-1], x[i]]](images/Newton_Leibniz_36.gif) intervallumnak van olyan belsõ
intervallumnak van olyan belsõ ![xi[i]](images/Newton_Leibniz_37.gif) pontja, amelyre:
pontja, amelyre:
![(F(x[i])-f(x[i-1]))/(x[i]-x[i-1])](images/Newton_Leibniz_38.gif) =
= ![eval(Diff(F(x), x), x = xi[i]) = f(xi[i])](images/Newton_Leibniz_39.gif) ,
,
ahol 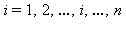 .
.
Vegyük a Lagrange-tétel által meghatározott közelítõ összegeket, vagyis minden egyes részintervallumban a ![xi[i]](images/Newton_Leibniz_41.gif) kiválasztott változóérték legyen a Lagrange tételben szereplõ
kiválasztott változóérték legyen a Lagrange tételben szereplõ ![xi[i]](images/Newton_Leibniz_42.gif) :
:
![sigma(n) = Sum(f(xi[i])*(x[i]-x[i-1]), i = 1 .. n)](images/Newton_Leibniz_43.gif) =
= ![Sum((F(x[i])-F(x[i-1]))/(x[i]-x[i-1]), i = 1 .. n)](images/Newton_Leibniz_44.gif) (
(![x[i]-x[i-1]](images/Newton_Leibniz_45.gif) ) =
) = ![Sum(F(x[i])-F(x[i-1]), i = 1 .. n)](images/Newton_Leibniz_46.gif) =
=
= (![F(x[1])-F(x[0])](images/Newton_Leibniz_47.gif) ) + (
) + (![F(x[2])-F(x[1])](images/Newton_Leibniz_48.gif) ) + . . . + (
) + . . . + (![F(x[n-1])-F(x[n-2])](images/Newton_Leibniz_49.gif) ) + (
) + (![F(x[n])-F(x[n-1])](images/Newton_Leibniz_50.gif) ) = (
) = (![F(x[n])-F(x[0])](images/Newton_Leibniz_51.gif) )=
)=
= 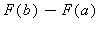
Tehát kaptuk, hogy
![sigma(n) = Sum(f(xi[i])*(x[i]-x[i-1]), i = 1 .. n)](images/Newton_Leibniz_53.gif) =
= 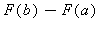
Ez azt jelenti, hogy az imént, Lagrange tétele alapján adódott speciális integrálközelítõ összegek azonosan egyenlõk az 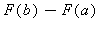 értékkel, tehát nyílván a határértékük is egyenlõ
értékkel, tehát nyílván a határértékük is egyenlõ 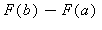 -val. De mi a helyzet más közelítõ összegek választása esetén? Tudjuk, a feltétel szerint az f függvény integrálható az
-val. De mi a helyzet más közelítõ összegek választása esetén? Tudjuk, a feltétel szerint az f függvény integrálható az ![[a, b]](images/Newton_Leibniz_57.gif) intervallumon, tehát tetszõleges -a határozott integrál definíciójában szereplõ feltételeket kielégítõ- integrálközelítõ összegeinek sorozata ugyanahhoz a számhoz konvergál. Az elõbbiek szerint ez a szám éppen
intervallumon, tehát tetszõleges -a határozott integrál definíciójában szereplõ feltételeket kielégítõ- integrálközelítõ összegeinek sorozata ugyanahhoz a számhoz konvergál. Az elõbbiek szerint ez a szám éppen 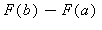 .
.
Ezzel a tétel bizonyítását befejeztük.
Példák
1. Példa
Számítsuk ki a következõ integrál értékét
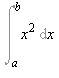
Megoldás
Az 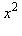 függvény egyik primitív függvénye az
függvény egyik primitív függvénye az 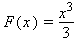 függvény. Ezért
függvény. Ezért
![(Typesetting:-mprintslash)([F := 1/3*x^3], [1/3*x^3])](images/Newton_Leibniz_62.gif)
| > |
Int(x^2,x=a..b)=subs(x=b,F)-subs(x=a,F); |
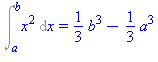
A Maple-lel közvetlenül kiszámítva:
| > |
Int(x^2,x=a..b)=int(x^2,x=a..b); |
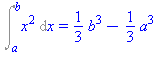
2. Példa
Számítsuk ki a következõ integrál értékét
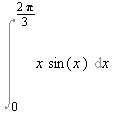
Megoldás
1. Megoldás
Elõször, parciális integrálással meghatározunk egy primitív függvényt, majd alkalmazzuk a Newton-Leibniz tételt.
| > |
Int(x*sin(x),x)=intparts(Int(x*sin(x),x),x); |
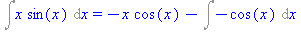
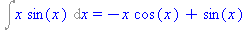
Képezzük ezután az 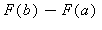 kifejezést. Helyettesítsünk a primitív függvényben az x helyére
kifejezést. Helyettesítsünk a primitív függvényben az x helyére 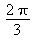 -at, majd 0-t, s képezzük az így nyert két érték különbségét!
-at, majd 0-t, s képezzük az így nyert két érték különbségét!
| > |
Int(x*sin(x),x = 0 .. 2*Pi/3)=subs(x=2*Pi/3,rhs(%))-subs(x=0,rhs(%)); |
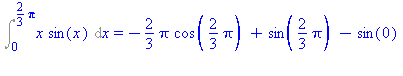
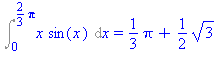
2. Megoldás
A parciális integrálás módszerét határozott integrál kiszámítására is alkalmazhatjuk:
| > |
Int(x*sin(x),x=0..2*Pi/3)=intparts(Int(x*sin(x),x=0..2*Pi/3),x); |
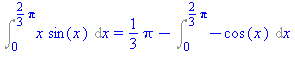
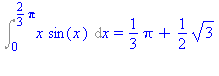
3. Megoldás
A Maple az integrál értékét közvetlenül is megadja:
| > |
Int(x*sin(x),x=0..2*Pi/3)=int(x*sin(x),x=0..2*Pi/3); |
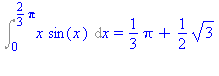
3. Példa
Számítsuk ki az alábbi integrált
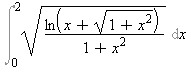
Megoldás
Próbáljuk elõször a Maple segítségével megadni az integrál pontos értékét!
| > |
Int(sqrt(ln(x+sqrt(1+x^2))/(1+x^2)),x=0..2); |
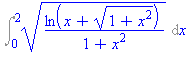
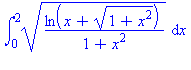
A Maple közvetlenül nem tudja kiszámítani az integrál értékét. Próbáljunk segíteni! Nézzük a gyök alatti kifejezés számlálójának deriváltját!
| > |
Diff(ln(x+(1+x^2)^(1/2)),x)=diff(ln(x+(1+x^2)^(1/2)),x); |
![(Typesetting:-mprintslash)([Diff(ln(x+(1+x^2)^(1/2)), x) = (1+x/(1+x^2)^(1/2))/(x+(1+x^2)^(1/2))], [Diff(ln(x+(1+x^2)^(1/2)), x) = (1+x/(1+x^2)^(1/2))/(x+(1+x^2)^(1/2))])](images/Newton_Leibniz_78.gif)
Egyszerûsítsük a deriváltat!
| > |
Diff(ln(x+(1+x^2)^(1/2)),x)=simplify(diff(ln(x+(1+x^2)^(1/2)),x)); |
![(Typesetting:-mprintslash)([Diff(ln(x+(1+x^2)^(1/2)), x) = 1/(1+x^2)^(1/2)], [Diff(ln(x+(1+x^2)^(1/2)), x) = 1/(1+x^2)^(1/2)])](images/Newton_Leibniz_79.gif)
A derivált éppen az integrandus nevezõje. Célszerû tehát a 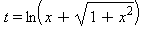 helyettesítés. A changevar eljárást a határozott integrál kiszámításakor is alkalmazhatjuk. Ekkor a helyettesítés során a határok is transzformálódnak, nem kell visszatérnünk az eredeti változóra. Elsõ lépésként elvégezzük a helyettesítést:
helyettesítés. A changevar eljárást a határozott integrál kiszámításakor is alkalmazhatjuk. Ekkor a helyettesítés során a határok is transzformálódnak, nem kell visszatérnünk az eredeti változóra. Elsõ lépésként elvégezzük a helyettesítést:
| > |
Int(sqrt(ln(x+sqrt(1+x^2))/(1+x^2)),x=0..2)=changevar(t=ln(x+(1+x^2)^(1/2)),Int(sqrt(ln(x+sqrt(1+x^2))/(1+x^2)),x=0..2),t); |
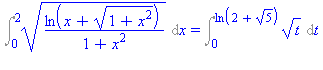
Számítsuk ki az integrál értékét:
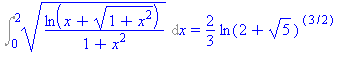
Az integrál értéke közelítõleg
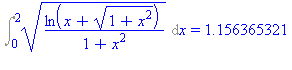
![]() az
az ![]() zárt intervallumon folytonos és
zárt intervallumon folytonos és ![]() amelyre
amelyre ![]() .
. 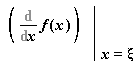 =
= ![]()
![]() hely, ahol a függvény változási sebessége egyenlõ az
hely, ahol a függvény változási sebessége egyenlõ az ![]() intervallumbeli átlagos változási sebességgel. Geometriailag ez azt jelenti, hogy az adott pontbeli érintõ párhuzamos az intervallum végpontjaihoz tartozó szelõvel.
intervallumbeli átlagos változási sebességgel. Geometriailag ez azt jelenti, hogy az adott pontbeli érintõ párhuzamos az intervallum végpontjaihoz tartozó szelõvel. ![]() eljesíti a Lagrange tétel feltételeit, hiszen a színusz függvény a valós számos halmazán deriválható és így ott folytonos is.
eljesíti a Lagrange tétel feltételeit, hiszen a színusz függvény a valós számos halmazán deriválható és így ott folytonos is. 
![]()

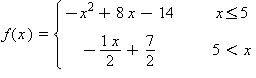
![]()
![(Typesetting:-mprintslash)([f(x) = PIECEWISE([-x^2+8*x-14, x <= 5], [x^2-7*x+11, 5 < x])], [f(x) = piecewise(x <= 5, -x^2+8*x-14, 5 < x, x^2-7*x+11)])](images/Newton_Leibniz_15.gif)

![]() intervallumon, az
intervallumon, az ![]() helyen azonban nem differenciálható.
helyen azonban nem differenciálható. ![]()
![]()
![]()

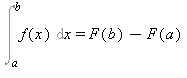
![(F(x[i])-f(x[i-1]))/(x[i]-x[i-1])](images/Newton_Leibniz_38.gif) =
= ![eval(Diff(F(x), x), x = xi[i]) = f(xi[i])](images/Newton_Leibniz_39.gif) ,
, ![sigma(n) = Sum(f(xi[i])*(x[i]-x[i-1]), i = 1 .. n)](images/Newton_Leibniz_43.gif) =
= ![Sum((F(x[i])-F(x[i-1]))/(x[i]-x[i-1]), i = 1 .. n)](images/Newton_Leibniz_44.gif) (
(![Sum(F(x[i])-F(x[i-1]), i = 1 .. n)](images/Newton_Leibniz_46.gif) =
= ![sigma(n) = Sum(f(xi[i])*(x[i]-x[i-1]), i = 1 .. n)](images/Newton_Leibniz_53.gif) =
= 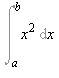
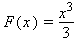 függvény. Ezért
függvény. Ezért 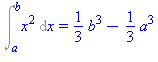
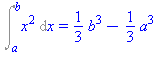
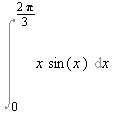
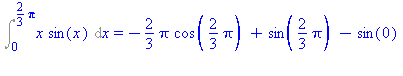
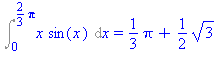
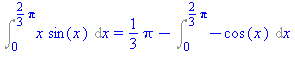
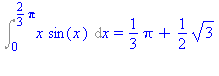
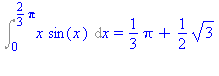
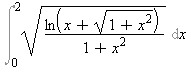
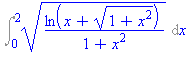
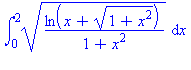
![(Typesetting:-mprintslash)([Diff(ln(x+(1+x^2)^(1/2)), x) = (1+x/(1+x^2)^(1/2))/(x+(1+x^2)^(1/2))], [Diff(ln(x+(1+x^2)^(1/2)), x) = (1+x/(1+x^2)^(1/2))/(x+(1+x^2)^(1/2))])](images/Newton_Leibniz_78.gif)